actividades.

ensayo :)

Por qué es tan difícil resolver problemas de razonamiento con incógnitas?

Muchas de la veces lo alumnos jóvenes como nosotros no comprendemos muy bien los problemas que contiene incógnitas ya que no tienen algún procedimiento o proceso el cual nos facilite su comprensión, por lo cual existe el método de “POYLA” el cual facilita todo problema de razonamiento matemático en la vida cotidiana el cual consiste en solo 4 pasos los cuales se deben seguir correctamente para su correcta comprensión y facilitación del problema, los pasos son los siguientes:

1)   Entender el problema: que es lo que te está preguntando, y que datos se cuenta.

2)   Elaborar un plan de trabajo: que es obtener las ecuaciones para la realización del problema

3)   Ejecutar el plan : se realiza la ecuación y su resolución

4)   Examinar la solución obtenida: aquí se realizan comprobación para saber si el resultado está bien.

Y con estos pasos se lleva a la solución de un problema en particular de una manera más sencilla, con el seguimiento de estos pasos.

En las diapositivas vistas se presenta un ejercicio de razonamiento, en el cual se resuelve de 3 maneras distintas tomando la incógnita en diferentes cosas.

Lizbeth Eduviges compró un vestido, unos zapatos y una bolsa de mano para su graduación gastando un total de $3800. Si la bolsa costó el doble que los zapatos y el vestido costó $550 más que la bolsa, ¿cuánto costó cada artículo?

En la primero presentación en el ejercicio se toma como incógnita los zapatos y es representado como “x” en la cual es mucho más fácil buscar el precio de los zapatos ya que de los zapatos no tenemos ningún dato y es así más sencillo sacar su precio total.

En la segunda presentación se toma como incógnita la bolsa que se representa como “x” en este caso a mí se me dificulta más ya que el dato que tenemos es que la bolsa costo el doble del costo de los zapatos, y por lo cual en este problema se tendría que sacar el precio de los zapatos, para después poder sacar el precio de la bolsa, esto es aun confuso ya que se tendrían que hacer más operaciones para su resolución y esto conllevaría la utilización ya de fracciones.

En la tercera presentación es un caso con mucha más dificultad para mí ya que como incógnita se toma el vestido y se representa con “x” esto es mucho más dificultad para poder realizarlo, ya que para poder sacar su precio tendríamos que sacar el precio de los zapatos y de la bolsa para poder llegar al resultado final. 

funciones lógicas :)

En qué consiste el formato condicional?

El formato condicional en Excel nos permite aplicar de manera selectiva un formato a las celdas de acuerdo a su contenido. Este formato se aplicará de manera automática sobre la celda después de evaluar el cumplimiento de la regla de formato condicional.

La función buscar en v

La función BUSCARV en Excel nos permite buscar un valor dentro de un rango de datos, es decir, nos ayuda a obtener el valor de una tabla que coincide con el valor que estamos buscando. Un ejemplo sencillo que podemos resolver con la función BUSCARV es la búsqueda dentro de un directorio telefónico.

Si queremos tener éxito para encontrar el teléfono de una persona dentro del directorio telefónico de nuestra localidad debemos tener el nombre completo de la persona. Posteriormente habrá que buscar el nombre dentro del directorio telefónico para entonces obtener el número correcto.

Función buscar en h

La función BUSCARH en Excel busca un valor dentro de una fila y devuelve el valor que ha sido encontrado o un error #N/A en caso de no haberlo encontrado. Esta función es similar, en cierto sentido, a la función BUSCARV.

Debemos utilizar la función BUSCARH cuando el valor que estamos buscando se encuentra en una fila de alguna tabla de datos. Por el contrario, la función BUSCARV realiza la búsqueda en una columna.

Función de las tablas dinámicas en Excel

Las tablas dinámicas en Excel permiten agrupar datos en una gran cantidad de maneras diferentes para  poder obtener la información que necesitamos. En esta ocasión explicaré el funcionamiento básico de una tabla dinámica.

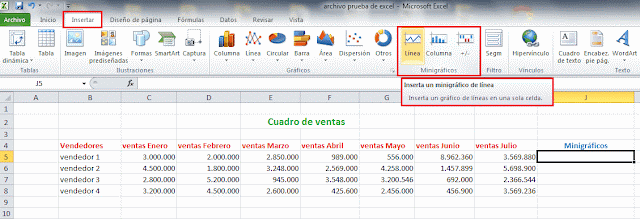
Supongamos que tienes una tabla de datos que contiene mucha información sobre las ventas de la compañía entre las cuales se encuentra una columna con los productos de la empresa, también la ciudad donde se vende y las ventas correspondientes para cada ciudad.

Funciones lógicas en Excel

Las funciones lógicas en Excel se utilizan en la toma de decisiones. En base al resultado de una función decidiremos si ejecutar o no cierta acción requerida.

FUNCIÓN	INGLÉS	DESCRIPCIÓN
FALSO	FALSE	Devuelve el valor lógico FALSO.
NO	NOT	Cambia FALSO por VERDADERO y VERDADERO por FALSO.
O	OR	Comprueba si alguno de los argumentos es VERDADERO y devuelve VERDADERO o FALSO. Devuelve FALSO si todos los argumentos son FALSO.
SI	IF	Comprueba si se cumple una condición y devuelve un valor si se evalúa como VERDADERO y otro valor si se evalúa como FALSO.
SI.ERROR	IFERROR	Devuelve un valor si la expresión es un error y otro valor si no lo es.
VERDADERO	TRUE	Devuelve el valor lógico VERDADERO.
Y	AND	Comprueba si todos los argumentos son VERDADEROS y devuelve VERDADERO o FALSO. Devuelve FALSO si alguno de los argumentos es FALSO.

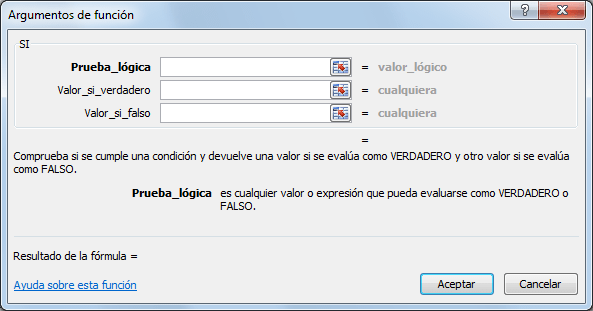
Función lógica “si”

La función SI en Excel es parte del grupo de funciones Lógicas y nos permite evaluar una condición para determinar si es falsa o verdadera. La función SI es de gran ayuda para tomar decisiones en base al resultado obtenido en la prueba lógica.

La Prueba lógica puede ser una expresión que utilice cualquier operador lógico o también puede ser una función de Excel que regrese como resultado verdadero o falso.

Los argumentos Valor si verdadero y Valor si falso pueden ser cadenas de texto, números, referencias a otra celda o inclusive otra función de Excel que se ejecutará de acuerdo al resultado de la Prueba lógica.

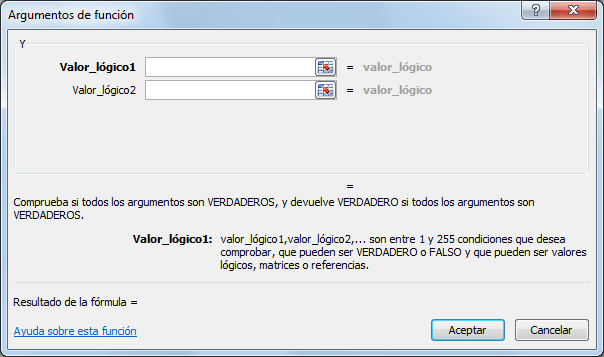
Función lógica “Y”

La función Y en Excel es una función lógica que nos permitirá evaluar varias expresiones lógicas y saber si todas ellas son verdaderas. Será suficiente con que cualquiera de las expresiones sea falsa para que el resultado de la función también sea falso.

La función Y solamente regresará el valor verdadero si todas las expresiones lógicas evaluadas son verdaderas. Bastará con que una sola expresión sea falsa para que la función Y tenga un resultado falso.

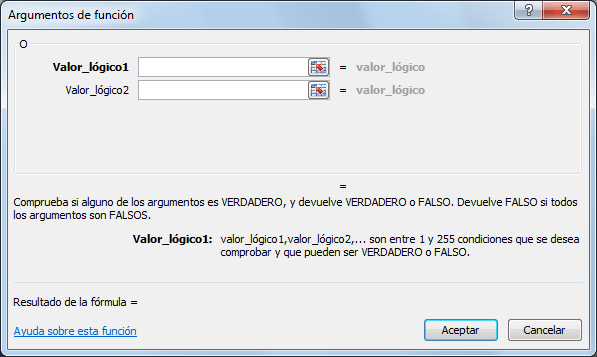
Función lógica “o”

Es una de las funciones lógicas de Excel y como cualquier otra función lógica solamente devuelve los valores verdadero o falso después de haber evaluado las expresiones lógicas que se hayan colocado como argumentos.

La única manera en que la función O devuelva el valor falso es que todas las expresiones lógicas sean falsas. Si al menos una expresión es verdadera entonces el resultado de la función O será verdadero.

actividad 4 :) .

ensayo - etapas del desarrollo del álgebra

Etapas del desarrollo del álgebra

Se dice que el álgebra es una ciencia la cual es la rama más importante de las matemáticas  y tiene relación entre cantidades, magnitudes y propiedades ya es utilizada para reducir estas mismas.

El álgebra es importante ya que hace combinaciones de sobre números, letras signos.

En la historia del algebra relata sobre sus inicios donde sus primeros avances fueron en babilonia y Egipto a.c y estos las usaban para resolver problemas de primero y segundo grado

Después el álgebra su utilizada en la antigua Grecia, ellos la utilizaban para resolver tanto teoremas como ecuaciones, así efectuarla en el teorema de Pitágoras , y poco a poco el álgebra tomo otro camino ya que empezaron a incluir muchísimas más cosas como lo son partes de todas la teorías , ya que también le agregaron la algebra bilineal.

Aproximadamente en el año de 1800 antes de cristo Strassburg de babilonia buscaba la solución de una ecuación elíptica cuadrática.

En al año de 1600 antes de cristo Plimpton 322 da una tabla de ternas pitagóricas en escritura cuneiforme babilónica.

Año 800 antes de cristo un matemática llamado Baudhayana un día descubre 3 Pitágoras en la algebraica, en la misma encontró soluciones con una formula la cual es esta x2 = c y ax2 + bx = c, y además encontró otras dos soluciones positivas con ecuaciones diofanticas simultáneas.

Año 600 antes de cristo un matemático hindú encuentra y resuelve la ecuación lineal y además utilizo la ecuaciones diofanticas hasta con 4 o 5 incógnitas.

Año 300 antes de cristo en un libro tomo ll, un matemático llamado Euclides da una construcción  geométrica para resolver la ecuación cuadrática para sus  raíces  positivas.

También en el año 300 antes de cristo se busca una forma de resolver las ecuaciones cubicas.

Año 100 antes de cristo las ecuaciones algebraicas se tratan en el suanshu chino de Jiuzhang del libro de las matemáticas este mismo libro contiene las soluciones de las ecuaciones lineares usando como su solución un método llamado la regla falsa.

También en el año 100 antes de cristo El manuscrito de Bakhshali utilizaba una notación algebraica, en la cual eran utilizadas letras del alfabeto, las cuales eran ecuaciones cubicas y de cuarto grado.

Año 200 el matemático Diofanto, de Egipto mejor conocido como el padre del algebra dio a conocer su trabajo aritmético que contenía las soluciones de ecuaciones algebraicas y las famosa teoría de los números.

En el año 625 un matemático de origen chino dio a conocer la soluciones de las ecuaciones cubicas.

Año 850 el al-Mahani persa del matemático dijo su grandiosa idea de simplificar  los problemas geométricos, como duplicarle el cubo a los problema en el álgebra.

Año 1114 Bhaskara , después de tanto investigar reconoció  que un número tiene raíz cuadrada tanto positiva como negativa.

   Etapas del álgebra  

Álgebra retórica: que fue desarrollada por los babilónicos, en esta fue la etapa más fácil ya que se componía por solo números naturales sin símbolos ni ecuaciones, no se utilizaba nada de esto es por eso que fue la inicial y la más práctica, para todos. También llamada algebra clásica.

Álgebra sincopada: esta es la segunda etapa, según lo desarrollado por Diofanto y el manuscrito de Bakhshali. En esta etapa ya se usaban abreviaciones para plantear las incógnitas y ya sería un lenguaje del algebra un poco más complicado ya que tendría abreviaturas para saber el problema, pero no su solución.

Álgebra simbólica: se considera su culminación con el trabajo de Leibniz.

En esta ya se le habían agregado letras llamadas literales, para las incógnitas.

http://www.taringa.net/post/apuntes-y-monografias/1722612/Algebra.html

ttps://www.clubensayos.com/Historia/Etapas-Del-Algebra/55320.html

http://es.slideshare.net/JazminRivera2/etapas-del-desarrollo-del-algebra

500 palabras acerca de los vídeos y su perspectiva

Estudiantes no mexicanos

En la perspectiva de los estudiantes no mexicanos muestran el  día de muertos como una fiesta, no como tradición al tener que hacerlo cada día 2 , si no como un día de fiesta de celebrar y no recordar con dolor al ser amado , ya que muchas persona utilizan ese día para recordar con tristeza al ser amado y no lo ven como una fiesta en la cual todos los muertos son felices porque les llego su día , día de fiesta de celebrar con entusiasmo que están en un lugar mejor y en este vídeo así lo muestran ya que lo hacen festejando con todo lo que es la cultura mexicana ,que abarca lo que es romper la piñata, la comida mexicana , el melón y su artesanía, el baile y todo lo típico que hay en México para celebrar ese día tan importante. Es muy interesante que estos estudiantes no mexicanos lo vean así, ya que lo toman de una manera feliz.

Estudiantes mexicanos

En este caso los estudiantes mexicanos lo ven de una perspectiva muy real, ya que en estos tiempos el día de muertos lo vemos como una obligación y no un día de festejar a nuestros seres queridos y de visitarlos con cariño, no con obligación de ir.

En este este video toma aun personaje llamado pepe que en él se muestra la muerte como algo que temible, el temor a la muerte , al llegar hay a ese llegar y no saber qué hacer ante esa situación, pero en el video al llegar a las 12 se muestra como empieza la fiesta y su celebración para todos aquellos que sus familiares los recuerdan con cariño y les rinden tributo al hacerle su altar en cada una de sus casas , entonces cada uno de los muertos acuden a su celebración y en este caso pepe se queda solo ya que sus familiares lo olvidaron , y es se encuentra en el lugar a un anciano y ahí le dice si también lo olvidaron , hay se da cuenta que es su padre.

Esta perspectiva es real ya que nosotros como mexicanos entre más tiempo tengan muertos nuestros seres queridos más rápido los olvidamos y no los recordamos y ese día lo pasamos desapercibido.

Profesionales

En esta ultimo perspectiva que es la profesional, en este vídeo se muestra la muerte y el día de muertos con algo de dolor, con el hecho de pensar que ya no volverás a ver a esa persona importante, a ese ser amado, ya nunca jamás y dejaras un vacío muy grande, y estar recordando todo lo que se vivió con este, pero también te muestra la madurez para poder enfrentar las cosas y dejar atrás lo que ha pasado, por que en algún momento todos pasaremos por eso, y al fin entender que las cosas pasan por algo , porque son los ciclos de la vida, y todos llegaremos a estar ahí en ese lugar y reencontrarnos con los nuestros.

barra de herramientas de excel

Barra Inicio: incluye las funciones más comunes, como formato de texto y estilos, además de otras opciones

Portapapeles

Pegar.- Obtener opciones de como pegar únicamente los valores.

Cortar.- Corta la selección del documento y la pega en Portapapeles.

Copiar.- Copia y coloca en Portapapeles.

Fuente

Fuente.- Tipo de Letra.

Tamaño de Fuente.- Tamaño de la Letra.

Negrita.- Remarca un texto seleccionado.

Cursiva.- Letra en Cursiva.

Subrayado.- Subraya una parte de una hoja seleccionada.

Borde Inferior.- Coloca diferentes bordes a la hoja.

Color de Relleno.- Color que se coloca dentro de tabla, registro, fila.

Alineación

Orientación.- Gira el texto a un ángulo diagonal o vertical.

Disminuir Sangría y aumentar Sangría.- Margen entre el borde inferior y el texto de la celda.

Texto a la Izquierda.- Lugar donde se pondrá el texto

Centrado.- Texto colocada en el centro de la celda.

Ajustar Texto.- Hace que se vea visible.

Combinar y Centrar.- Une las celdas seleccionadas.

Número

Formato de Numero.- Designación a las cantidades en las celdas.

Formato de Numero de Contabilidad.- Se representara en unidades monetarias.

Estilo Porcentual.- Se representara en porcentajes.

Estilos

Formato Condicional.- Resalta celdas interesantes.

Dar Formato como Tabla.- Convierte celdas seleccionadas en Tablas.

Celdas

Insertar.- Insertar nuevas celdas.

Eliminar.-Eliminar celdas.

Formato.- Cambia el alto de las filas o el ancho de las columnas.

Modificar

Autosuma.-Muestra la suma de celdas seleccionadas.

Rellenar.- Rellena de celdas en cualquier dirección.

Borrar.- Borra celdas.

Buscar y Seleccionar.- Búsqueda de partes específicas.

*Barra Insertar: básicamente engloba todas las posibilidades de incorporar contenido a nuestra hoja de cálculo, desde imágenes, tablas, vínculos, ecuaciones, etc.

Tablas

Tablas Dinámica.- Resume datos usando una tabla dinámica.

Tabla.- Crear tablas.

Ilustraciones

Imagen.- Insertar una imagen.

Imagen Prediseñadas.- Colocar una imagen prediseñada.

Formas.- Colocar formas, como líneas, flechas,etc.

SMARTART.- Incluye diagramas especializados, listas.

Gráficos

Columna.- Representar en forma de columnas.

Línea (Se utiliza para datos de tendencias en el Tiempo.

Circular.- Representar información en forma de círculos.

Barra.-Se utiliza para la comparación.

Área.- Se utiliza para representar información en periodos de Tiempo.

Vínculos

Hipervínculos.-Para establecer vínculos con páginas web.

Texto

Cuadro de Texto.- Insertar cuadros de texto.

Encabezado y pie de Página.- Insertar.

WORDART.- Texto decorativo.

Objeto.- Inserta objetos incrustados.

Símbolo.-Inserta caracteres que no hay en el Teclado.

* Barra Diseño de página: Permite diseñar la forma y el tamaño de la hoja, entre otras opciones

Temas

Temas.- Cambia el tema del documento.

Colores.- Modifica los colores de la hoja.

Fuentes.-Modifica las fuentes de la hoja.

Efectos.-Modifica los efectos de la hoja.

Configurar Pagina

Márgenes.- Selecciona el tamaño del margen.

Orientación.-El diseño horizontal o vertical.

Tamaño.- El tamaño del papel.

Área de impresión.-Marca un área especifica de la hoja para imprimirla.

Saltos.-Especifica el inicio de una nueva página en la copia de impresión.

Fondo.-Imagen para el fondo de la hoja.

Imprimir Títulos.-Especifica filas y columnas.

Ajustar Área de Impresión

Ancho.- Reduce el ancho de impresión.

Alto.-Reduce al alto de impresión.

Escala.-Aumenta o disminuye el resultado de impresión en un porcentaje.

Opciones de Hoja

Líneas de la Cuadricula

Ver.- Muestra las líneas entre filas y columnas de la hoja.

Imprimir.-Imprime las líneas entre las filas y columnas de la hoja.

Organizar

Panel de Selección.-Selección de objetos.

Alinear.-Alinea los bordes de varios objetos seleccionados

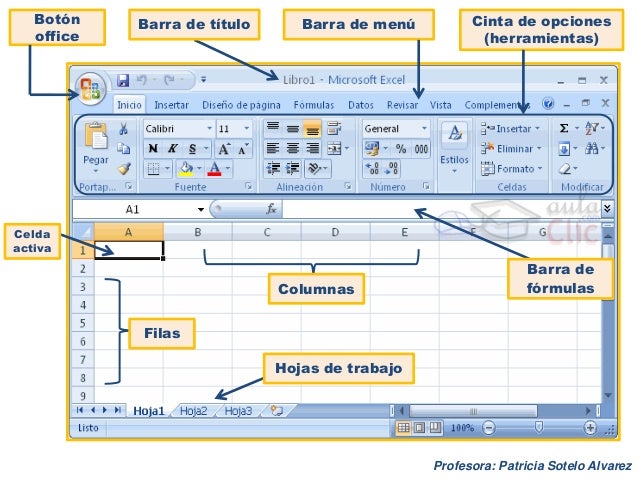
entorno de excel

Entorno Excel

Como todos los programas de Office (Word, Excel, Power Point y Access) tienen un entorno parecido, es decir todos tienen menú, barra de herramientas, barra de estado, barra de dibujo. Y Excel tiene una barra importante que es la barra de fórmulas, que utiliza para visualizar y modificar datos insertados en una celda.

INSTRUCTIVO                  

Memórama algebraico.

Objetivo: conocer y aprender los conceptos básicos del álgebra para el mejor aprendizaje del mismo.

Este es el clásico juego del memórama en el cual aprenderás algunos conceptos que te ayudaran en el aprendizaje del mismo.

·         Para poder jugar es necesario seguir las siguientes instrucciones para su comprensión:

1)      Sacar todas las tarjetas de la caja (40 piezas).

2)      Cada uno de los integrantes del equipo ayudara a revolver las tarjetas, para la realización del juego.

3)      Poner las tarjetas hacia abajo de modo que no se vea el concepto y respuesta.

4)      Cada jugador tendrá su turno para tomar una tarjeta en la cual deberá en encontrar ya sea el concepto y después su respuesta o a la inversa primero la respuesta y después el concepto.

Nota: En la siguiente tabla están las respuestas correctas.

Concepto	Definición
Concepto de termino algebraico	Toda expresión algebraica cuyas partes no están separadas por los signos + o - .
Concepto de signo	Se refiere a la propiedad de ser positivo o negativo.
Concepto de coeficiente	Es un factor multiplicativo. Es el número constante que se encuentra ala izquierda de una variable o incógnita.
Concepto de variable	Es un símbolo para un número que aún no sabemos. Es normalmente una letra como   x o y.
Concepto de exponente	Es el que representa un número y muestra cuantas veces el número se va a utilizar en la multiplicación ejemplo  =8x8 =64
Concepto de monomio	Es un polinomio pero con un solo término. Ejemplo
Concepto de binomio	Es un polinomio pero con dos términos. Ejemplo - 2
Concepto de trinomio	Es un polinomio pero con tres términos. Ejemplo --2
Concepto de polinomio	Es una expresión hecha con constantes, variables y exponentes, que se están combinando u usando sumas, restas y multiplicaciones, pero no divisiones. Los exponentes solo pueden ser 0, 1, 2,3,…. Etc.
Concepto de grado respecto a una variable	Se conoce como grado del polinomio. Es el exponente de mayor orden de la variable. Ejemplo +-2. y 4 es el exponente de mayor orden .
Ejemplo de polinomio con más de tres términos	a)     4ax4y3+x2y+3ab2y3 b)     4x4-2x3+3x2-2x+5
Concepto de grado absoluto	Operación matemática realizada sobre una expresión algebraica. Se obtiene con la suma de los exponentes de todas las variables. Ejemplo ()= 2+5+6 =13
Literales utilizadas como constantes	Son las letras, pueden ser cualquiera, la A, la B,C,D pero la que más se utiliza es expresión X
Concepto de expresión algébrica	Es una enunciación matemática formada por los números y por símbolos representados por letras.  (Indicadores de incógnitas).
Ejemplos de términos semejantes	a)     3xy-xy b)      ab+3ab
Ejemplo de termino absoluto con grado 6	es de grado absoluto 6
Ejemplo de binomio	=
Ejemplo de termino con grado 3 respecto a equis	y
Ejemplo de termino con grado 3 respecto a ye
Concepto de trinomio	Es un polinomio que consta de 3 monomios. Ejemplo p(x) 2x+3x+5

5)      El primer jugador levantara una tarjeta y por consiguiente tendrá que encontrar su respuesta correcta, en caso de que no sea así devolver  la tarjeta a su lugar.

6)      Para siguiente paso el jugador que tenga el siguiente turno levantara la tarjeta que más desee y encontrara la respuesta correcta , dado que ese sea el caso ,seguirá levantando tarjetas , hasta ya no encontrar las respuestas correctas. Y seguirá el turno del siguiente jugador.

7)      El jugador con el 3 turno ya tendrá más ventaja al sacar las tarjetas ya que estuvo haciendo memoria de donde están las tarjetas que se han estado volteando, y con esto se hace referencia al juego del MEMORAMA.

8) Todos los jugadores al terminar deberán contar sus pares y el ganador será el que haya obtenido más pares.